在金融市场中，行情判断的能力直接决定了策略的盈利能力。盈利的关键并不在顺风行情中赚得更多，而是在逆风行情中亏得更少。由于市场极端行情往往不会回头，许多投资者在面对突发行情时容易陷入幻想，从而加剧亏损。

策略并非万能，每种策略都有其适用性。例如： - 趋势策略在单边行情中表现优异，但在震荡行情中可能因为频繁止损而亏损； - 震荡策略在趋势行情中容易因单边持仓导致损失。

因此，判断行情类型（趋势或震荡）至关重要，这直接决定了策略选择的有效性和盈利能力。

行情判断方法：从主观到量化

传统上，许多交易者通过经验和直觉来判断行情，这种主观性判断容易受到情绪和偏见的干扰，存在很大的不确定性。为了解决这一问题，量化方法应运而生。通过引入统计学和数学模型，我们可以更客观地分析市场特征。

以下将介绍三种常用的量化方法：
1. CMI（Choppy Market Index）
2. ADX（Average Directional Index）
3. 时间序列分析法

1. CMI（Choppy Market Index）

CMI 是一种衡量市场波动性和趋势性的指标，能直观地显示市场状态。

其公式为：

[ CMI = \frac{\text{ATR} \times 100}{\text{High}_N - \text{Low}_N} ]

其中：
- (\text{ATR})：真实波动范围（Average True Range），衡量价格波动幅度；
- (\text{High}_N) 和 (\text{Low}_N)：最近 (N) 个周期内的最高价和最低价。

CMI 的特点： - CMI 值较高时，表示市场有较强的趋势性； - CMI 值较低时，表示市场处于震荡状态。

为了更清楚地理解其运作，我们实现了以下代码：

def cmi_calculate(data, window_size, cmi_threshold):
    """
    计算 Choppy Market Index (CMI) 并判断市场状态
    """
    # 获取数据
    high_prices = data['High'].values
    low_prices = data['Low'].values
    close_prices = data['Close'].values

    cmi_values = [None] * len(data)
    point_states = ['Unknown'] * len(data)

    # 滑动窗口计算 CMI
    for i in range(window_size, len(data)):
        high_window = high_prices[i - window_size + 1:i + 1]
        low_window = low_prices[i - window_size + 1:i + 1]
        close_window = close_prices[i - window_size + 1:i + 1]

        hh = high_window.max()
        ll = low_window.min()
        cmi = abs((close_window[-1] - close_window[0]) / (hh - ll)) * 100 if hh != ll else 0
        cmi_values[i] = cmi

        # 根据阈值分类
        point_states[i] = 'Trend' if cmi > cmi_threshold else 'Oscillation'

    return cmi_values, point_states

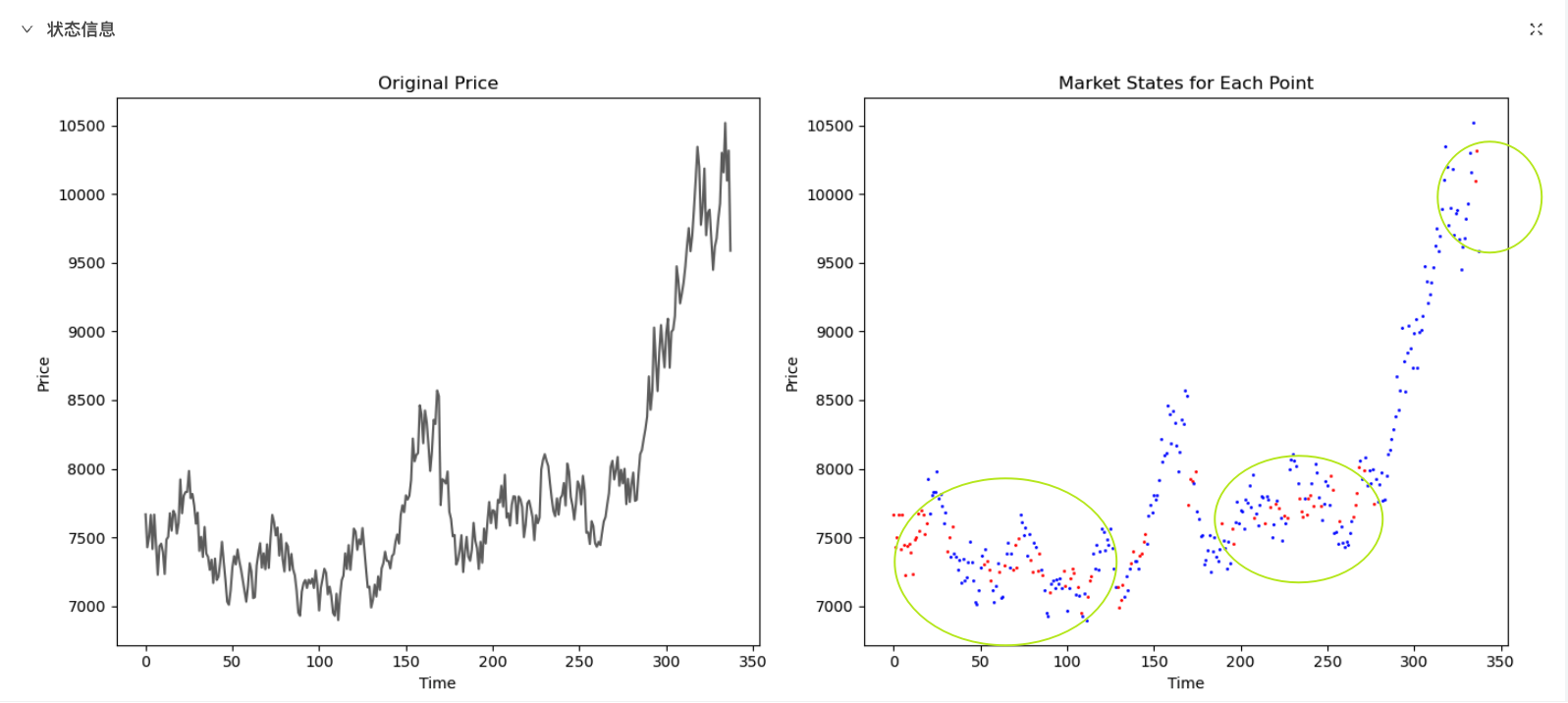
2. ADX（Average Directional Index）

CMI 能直观地分类市场状态，而 ADX 则专注于衡量趋势的强度，适用于更复杂的市场分析。

其计算公式为：

[ ADX = \frac{\text{EMA}(\text{DI}^+ - \text{DI}^-)}{\text{TR}} ]

其中：
- (\text{DI}^+) 和 (\text{DI}^-)：分别为正向和反向动量指标；
- (\text{TR})：真实波动范围。

ADX 的特点： - ADX 值高于某阈值（如 25）时，表明市场存在明显趋势；
- ADX 值较低时，表明市场震荡。

以下是 ADX 的实现代码：

def adx_calculate(data, window_size=20, adx_threshold=25):
    """
    计算 ADX 并判断市场状态
    """
    # 使用 TA-Lib 进行 ADX 计算
    adx = talib.ADX(data['High'].values, data['Low'].values, data['Close'].values, timeperiod=window_size)

    # 根据阈值判断市场状态
    point_states = ['Trend' if adx[i] > adx_threshold else 'Oscillation' for i in range(len(adx))]

    return adx, point_states

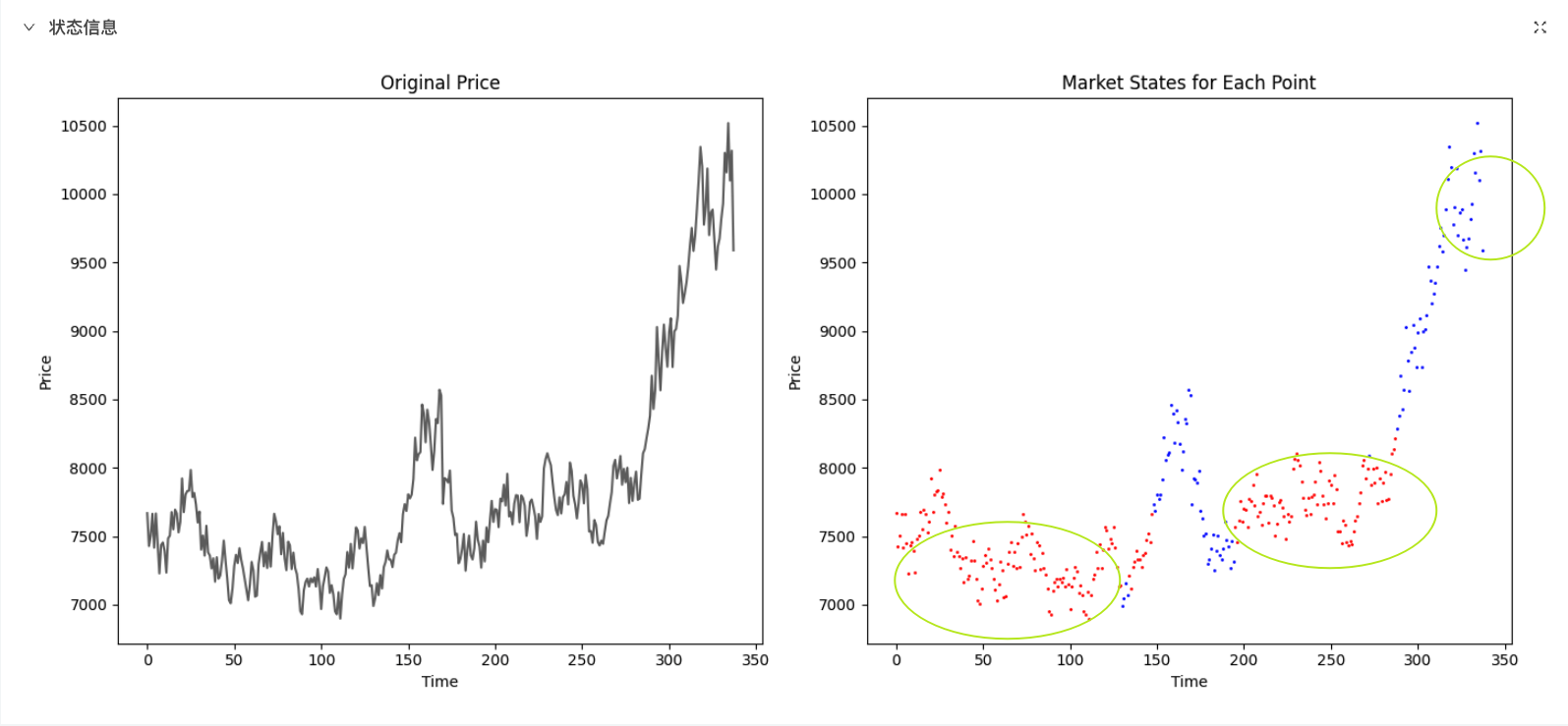
3. 时间序列分析法

如果希望通过统计分析进一步提高判断的精度，可以使用时间序列方法。这种方法的核心是检测价格序列的平稳性和自相关性：

1. ADF（Augmented Dickey-Fuller Test）

   • 检验时间序列是否存在单位根（非平稳）。
     
   • 非平稳序列通常代表趋势市场。

2. ACF（Autocorrelation Function）

   • 检测序列的自相关性。
     
   • 趋势序列通常自相关性较强。

以下是代码实现：

from statsmodels.tsa.stattools import adfuller, acf

def analyze_market_states(data, window_size=20, threshold_adf=0.05, threshold_acf1=0.6, threshold_acf2=0.4):
    """
    通过 ADF 和 ACF 区分市场状态
    """
    def adf_test(series):
        result = adfuller(series)
        return result[1]

    def acf_test(series):
        acf_values = acf(series, nlags=2)
        return acf_values[1] > threshold_acf1 and acf_values[2] > threshold_acf2

    point_states = ['Unknown'] * len(data)

    for i in range(len(data) - window_size + 1):
        window = data[i:i + window_size]
        p_value = adf_test(window)

        if p_value > threshold_adf and acf_test(window):
            point_states[i + window_size // 2] = 'Trend'
        else:
            point_states[i + window_size // 2] = 'Oscillation'

    return point_states

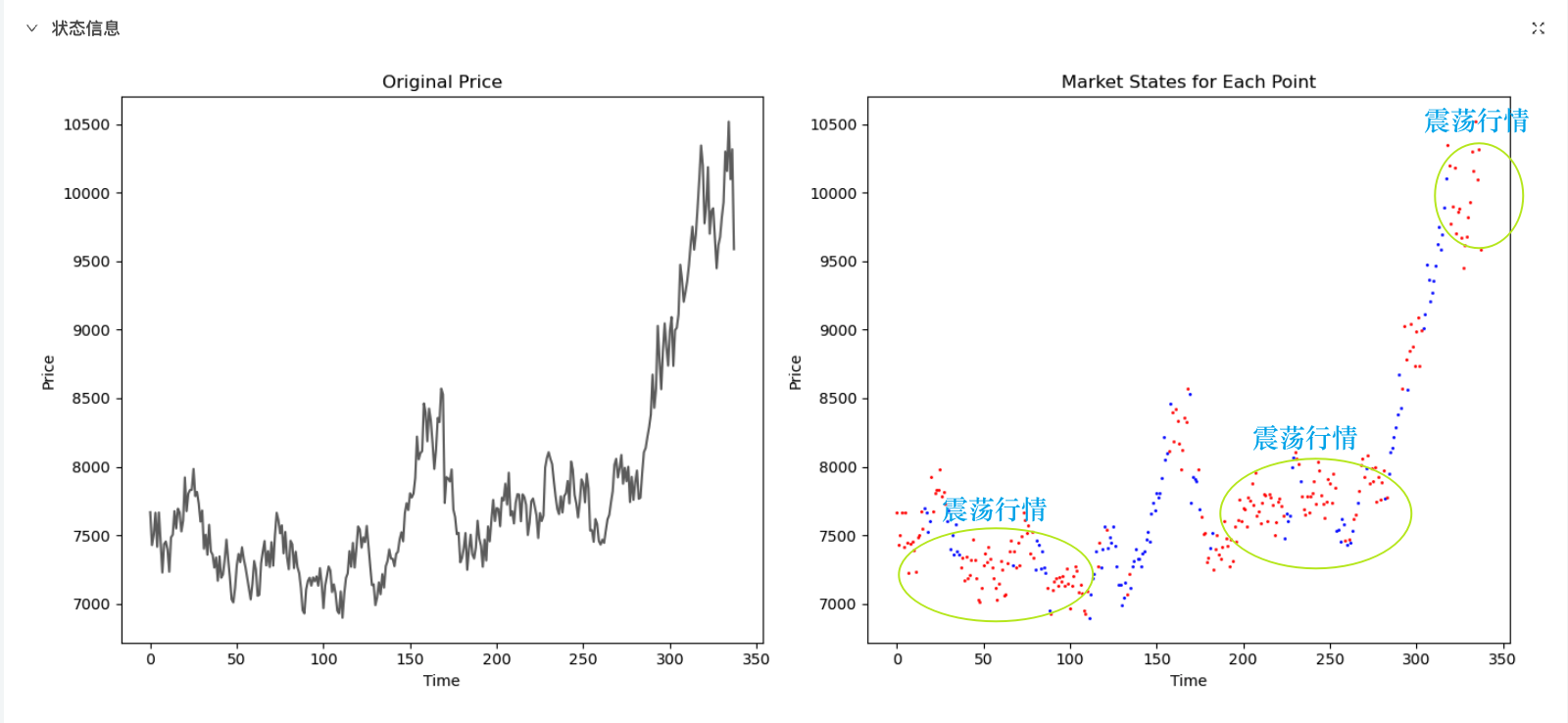
三种方法对比与结论

以 2024 年棕榈油期货行情为例，在优宽量化平台，我们对比了 CMI、ADX 和时间序列分析三种方法的效果：

1. CMI：

   • 优点：简单直观，适合快速判断。
   • 缺点：对极端行情较为敏感。

2. ADX：

   • 优点：衡量趋势强度，适用范围广。
   • 缺点：滞后性较强。

3. 时间序列分析：

   • 优点：统计精度高，抗干扰性强。
   • 缺点：计算复杂，对数据要求较高。

结论： 时间序列分析在分类效果上优于 CMI 和 ADX，但在高频交易中可能因计算开销较大而受限。对于实际应用，应结合不同市场和策略需求选择方法。

注：这里仅仅是针对于固定参数，我们可以使用不同的参数组合进行更多品种，更多行情的设置。

优化与扩展

• 调参与去噪：

  • 针对不同品种和行情优化参数。
  • 使用平滑技术降低数据噪声。

• 复杂方法：

  • 引入深度学习模型（如 LSTM）捕捉非线性特征。
  • 使用聚类算法识别隐含市场状态。

通过不断优化模型和结合多种方法，可以在复杂的市场中提高判断准确性，为策略执行提供可靠支持。