浅谈枢纽点理论在商品期货中的应用
 0
0
 407
407

枢轴点的历史背景
枢轴点(pivot point)是由一个华尔街知名机构经过长达7年的统计数据得出的结论,发现当天价格有不低于75%的时间会回到枢轴点中央价格线以上。交易员们非常重视这一结果,枢轴点成为了交易的重要依据,被广泛应用于日内交易和中长线交易中。目前,欧美银行、对冲基金在外汇、股票、指数、商品和加密货币的交易中广泛使用枢轴点。
枢轴点的形成和计算
枢轴点是精确的价格估计,通过一系列的算法,得出各个位置的支撑阻力价格。枢轴点分析是一种判断价格可能出现反应关键位的技术。枢轴点往往起着支撑或阻力的作用,并可能成为转折点。通常用于日内交易,但在不同时间框架下同样有效。大多数情况下,枢轴点使用一些重要价格的变化,比如已确立的高点(H)、低点(L)、和收盘价(C),通过计算来确定这些点。它们在枢轴点附近计算额外的支撑和阻力水平,用来确定何时进入或退出交易,或确定市场的范围。
枢轴点的计算公式
枢轴点一般常用形式包括3个关键点类型:Pivot Point(枢轴点),Support(支撑点),和 Resistance(阻力点)。具体的支撑和阻力点包括使用5点,7点甚至13点形式,用来划分不同的价格水平。
经典枢轴点(Classic Pivot Point)
介绍: 经典枢纽点是一种最常用的技术分析工具,用于确定潜在的支撑和阻力水平。这种方法使用前一个交易周期的高点、低点和收盘价来计算枢纽点及其相应的支撑和阻力位。交易员通常会使用这些水平来预测价格走势和制定交易策略。
主枢轴点(PP):
[ PP = \frac{(H + L + C)}{3} ]支撑位和阻力位:
- R1:[ R1 = 2 \times PP - L ]
- S1:[ S1 = 2 \times PP - H ]
- R2:[ R2 = PP + (H - L) ]
- S2:[ S2 = PP - (H - L) ]
- R3:[ R3 = H + 2 \times (PP - L) ]
- S3:[ S3 = L - 2 \times (H - PP) ]
伍迪枢轴点(Woodie Pivot Point)
介绍: 伍迪枢纽点是由Ken Wood开发的一种枢纽点计算方法。它在计算中给予收盘价更大的权重,这使得它更适用于日内交易。伍迪枢纽点被认为比经典枢纽点更敏感,因为它更关注最新的市场价格。
主枢轴点(PP):
[ PP = \frac{(H + L + 2 \times C)}{4} ]支撑位和阻力位:
- R1:[ R1 = 2 \times PP - L ]
- S1:[ S1 = 2 \times PP - H ]
- R2:[ R2 = PP + (H - L) ]
- S2:[ S2 = PP - (H - L) ]
- R3:[ R3 = H + 2 \times (PP - L) ]
- S3:[ S3 = L - 2 \times (H - PP) ]
斐波那契枢轴点(Fibonacci Pivot Point)
介绍: 斐波那契枢纽点结合了斐波那契数列的比例关系和传统的枢纽点计算方法。通过在枢纽点上添加斐波那契回撤水平(如38.2%、61.8%等),可以确定更多的支撑和阻力水平。这种方法在市场中较为流行,因为它结合了两种广泛认可的技术分析工具。
主枢轴点(PP):
[ PP = \frac{(H + L + C)}{3} ]支撑位和阻力位:
- R1:[ R1 = PP + (H - L) \times 0.382 ]
- S1:[ S1 = PP - (H - L) \times 0.382 ]
- R2:[ R2 = PP + (H - L) \times 0.618 ]
- S2:[ S2 = PP - (H - L) \times 0.618 ]
- R3:[ R3 = PP + (H - L) ]
- S3:[ S3 = PP - (H - L) ]
卡玛利拉枢轴点(Camarilla Pivot Point)
介绍: 卡玛利拉枢纽点由Nick Stott于20世纪80年代开发。这种计算方法与其他枢纽点方法不同,重点在于使用前一交易日的收盘价来计算多个支撑和阻力水平。卡玛利拉枢纽点的独特之处在于它引入了更紧密的支撑和阻力水平,适用于短线交易和快速波动的市场。
主枢轴点(PP):
[ PP = \frac{(H + L + C)}{3} ]支撑位和阻力位:
- R1:[ R1 = C + (H - L) \times 1.1 / 12 ]
- S1:[ S1 = C - (H - L) \times 1.1 / 12 ]
- R2:[ R2 = C + (H - L) \times 1.1 / 6 ]
- S2:[ S2 = C - (H - L) \times 1.1 / 6 ]
- R3:[ R3 = C + (H - L) \times 1.1 / 4 ]
- S3:[ S3 = C - (H - L) \times 1.1 / 4 ]
- R4:[ R4 = C + (H - L) \times 1.1 / 2 ]
- S4:[ S4 = C - (H - L) \times 1.1 / 2 ]
德马科枢纽点(DeMark Pivot Points)
介绍: 德马科枢纽点(DeMark Pivot Points)是一种由交易分析师 Tom DeMark 提出的枢轴点计算方法,主要用于确定潜在的支撑和阻力位。DeMark 枢轴点与其他常见的枢轴点计算方法相比,具有不同的计算逻辑,尤其是在计算关键水平时考虑了开盘价、最高价、最低价和收盘价的关系。德马科枢轴点通常用于日内交易者和短期交易者,以识别价格可能的转折点和关键水平。 1. 确定 X 值: - 如果收盘价(Close)低于开盘价(Open),则 ( X = H + 2L + C ) - 如果收盘价(Close)高于开盘价(Open),则 ( X = 2H + L + C ) - 如果收盘价(Close)等于开盘价(Open),则 ( X = H + L + 2C )
这里,H 是最高价(High),L 是最低价(Low),C 是收盘价(Close),O 是开盘价(Open)。
计算枢轴点(PP): [ PP = \frac{X}{4} ]
计算阻力位(R1): [ R1 = \frac{X}{2} - L ]
计算支撑位(S1): [ S1 = \frac{X}{2} - H ]
如何利用枢轴点进行交易
做趋势突破: 市场大部分走势是在支撑阻力水平区间做震荡运动,剩余时间则是突破原有的震荡区间走出单边趋势。盯住区间外的空间,因为区间外是利润最大的地方。
做反转点: 当价格到达极限的阻力位和支撑位时,大资金、庄家和大型基金等的平仓动作会导致行情反转。这时需要跟随主力的思维及动作做反转点交易。
做震荡高抛低吸: 在没有大的多头或空头入场情况下,价格围绕R1和S1之间围绕轴心运动。如果交易日价格在R1-S1之间运动,思考谁会在里面交易:做市商、算法交易的电脑和散户小白等。
枢轴点的交易策略
枢轴点突破策略: 价格突破枢轴点水平以上或以下以确定交易方向。突破枢轴点被视为看涨或看跌信号,寻找买入或卖出机会。
枢轴点反弹策略: 价格接近枢轴点水平时寻找反弹信号。如果价格在枢轴点水平附近交易,并且存在看涨烛台形态,考虑做多;存在看跌烛台形态时,考虑做空。
枢轴点反转策略: 价格在枢轴点水平处发生反转的信号。如果价格在枢轴点水平上方交易,并且存在看跌烛台形态,考虑做空;价格低于枢轴点水平,并存在看涨烛台形态时,考虑做多。
在实际交易中,结合自己的交易风格和偏好选择适合的枢轴点分析方法,并结合其他技术指标和基本面分析进行综合判断,以提高交易效果。始终谨慎对待风险,并根据实际情况做出决策。枢轴点分析只是辅助工具,不构成投资建议。
优宽量化代码实现:
以下是五种枢轴点的计算和绘制函数:
function classicpivot(Rdata){
var rdata = Rdata[Rdata.length - 1]
var pivot = (rdata['High'] + rdata['Low'] + rdata['Close'])/3
var r1 = 2 * pivot - rdata['Low']
var r2 = pivot + rdata['High'] - rdata['Low']
var r3 = rdata['High'] + 2 * (pivot - rdata['Low'])
var s1 = 2 * pivot - rdata['High']
var s2 = pivot - (rdata['High'] - rdata['Low'])
var s3 = rdata['Low'] - 2 * (rdata['High'] - pivot)
$.PlotMultRecords("经典枢纽点", "KLine", Rdata, {layout: 'single', col: 12, height: '1200px'})
$.PlotMultHLine("经典枢纽点", parseFloat(r3).toFixed(2), "R3", "red", "ShortDot")
$.PlotMultHLine("经典枢纽点", parseFloat(r2).toFixed(2), "R2", "red", "ShortDot")
$.PlotMultHLine("经典枢纽点", parseFloat(r1).toFixed(2), "R1", "red", "ShortDot")
$.PlotMultHLine("经典枢纽点", parseFloat(pivot).toFixed(2), "Pivot", "blue", "DashDot")
$.PlotMultHLine("经典枢纽点", parseFloat(s1).toFixed(2), "S1", "green", "ShortDot")
$.PlotMultHLine("经典枢纽点", parseFloat(s2).toFixed(2), "S2", "green", "ShortDot")
$.PlotMultHLine("经典枢纽点", parseFloat(s3).toFixed(2), "S3", "green", "ShortDot")
}
function woodiepivot(Rdata){
var rdata = Rdata[Rdata.length - 1]
var pivot = (rdata['High'] + rdata['Low'] + 2 * rdata['Close'])/4
var r1 = 2 * pivot - rdata['Low']
var r2 = pivot + rdata['High'] - rdata['Low']
var r3 = rdata['High'] + 2 * (pivot - rdata['Low'])
var s1 = 2 * pivot - rdata['High']
var s2 = pivot - (rdata['High'] - rdata['Low'])
var s3 = rdata['Low'] - 2 * (rdata['High'] - pivot)
$.PlotMultRecords("伍迪枢纽点", "KLine", Rdata, {layout: 'single', col: 12, height: '1200px'})
$.PlotMultHLine("伍迪枢纽点", parseFloat(r3).toFixed(2), "R3", "red", "ShortDot")
$.PlotMultHLine("伍迪枢纽点", parseFloat(r2).toFixed(2), "R2", "red", "ShortDot")
$.PlotMultHLine("伍迪枢纽点", parseFloat(r1).toFixed(2), "R1", "red", "ShortDot")
$.PlotMultHLine("伍迪枢纽点", parseFloat(pivot).toFixed(2), "Pivot", "blue", "DashDot")
$.PlotMultHLine("伍迪枢纽点", parseFloat(s1).toFixed(2), "S1", "green", "ShortDot")
$.PlotMultHLine("伍迪枢纽点", parseFloat(s2).toFixed(2), "S2", "green", "ShortDot")
$.PlotMultHLine("伍迪枢纽点", parseFloat(s3).toFixed(2), "S3", "green", "ShortDot")
}
function fibopivot(Rdata){
var rdata = Rdata[Rdata.length - 1]
var pivot = (rdata['High'] + rdata['Low'] + rdata['Close'])/3
var r1 = pivot + (rdata['High'] - rdata['Low']) * 0.382
var r2 = pivot + (rdata['High'] - rdata['Low']) * 0.618
var r3 = pivot + (rdata['High'] - rdata['Low'])
var s1 = pivot - (rdata['High'] - rdata['Low']) * 0.382
var s2 = pivot - (rdata['High'] - rdata['Low']) * 0.618
var s3 = pivot - (rdata['High'] - rdata['Low'])
$.PlotMultRecords("斐波那契枢纽点", "KLine", Rdata, {layout: 'single', col: 12, height: '1200px'})
$.PlotMultHLine("斐波那契枢纽点", parseFloat(r3).toFixed(2), "R3", "red", "ShortDot")
$.PlotMultHLine("斐波那契枢纽点", parseFloat(r2).toFixed(2), "R2", "red", "ShortDot")
$.PlotMultHLine("斐波那契枢纽点", parseFloat(r1).toFixed(2), "R1", "red", "ShortDot")
$.PlotMultHLine("斐波那契枢纽点", parseFloat(pivot).toFixed(2), "Pivot", "blue", "DashDot")
$.PlotMultHLine("斐波那契枢纽点", parseFloat(s1).toFixed(2), "S1", "green", "ShortDot")
$.PlotMultHLine("斐波那契枢纽点", parseFloat(s2).toFixed(2), "S2", "green", "ShortDot")
$.PlotMultHLine("斐波那契枢纽点", parseFloat(s3).toFixed(2), "S3", "green", "ShortDot")
}
function campivot(Rdata){
var rdata = Rdata[Rdata.length - 1]
var pivot = (rdata['High'] + rdata['Low'] + rdata['Close'])/3
var r1 = rdata['Close'] + (rdata['High'] - rdata['Low']) * 1.1/12
var r2 = rdata['Close'] + (rdata['High'] - rdata['Low']) * 1.1/6
var r3 = rdata['Close'] + (rdata['High'] - rdata['Low']) * 1.1/4
var r4 = rdata['Close'] + (rdata['High'] - rdata['Low']) * 1.1/2
var s1 = rdata['Close'] - (rdata['High'] - rdata['Low']) * 1.1/12
var s2 = rdata['Close'] - (rdata['High'] - rdata['Low']) * 1.1/6
var s3 = rdata['Close'] - (rdata['High'] - rdata['Low']) * 1.1/4
var s4 = rdata['Close'] - (rdata['High'] - rdata['Low']) * 1.1/2
$.PlotMultRecords("卡玛利拉枢纽点", "KLine", Rdata, {layout: 'single', col: 12, height: '1200px'})
$.PlotMultHLine("卡玛利拉枢纽点", parseFloat(r4).toFixed(2), "R4", "red", "ShortDot")
$.PlotMultHLine("卡玛利拉枢纽点", parseFloat(r3).toFixed(2), "R3", "red", "ShortDot")
$.PlotMultHLine("卡玛利拉枢纽点", parseFloat(r2).toFixed(2), "R2", "red", "ShortDot")
$.PlotMultHLine("卡玛利拉枢纽点", parseFloat(r1).toFixed(2), "R1", "red", "ShortDot")
$.PlotMultHLine("卡玛利拉枢纽点", parseFloat(pivot).toFixed(2), "Pivot", "blue", "DashDot")
$.PlotMultHLine("卡玛利拉枢纽点", parseFloat(s1).toFixed(2), "S1", "green", "ShortDot")
$.PlotMultHLine("卡玛利拉枢纽点", parseFloat(s2).toFixed(2), "S2", "green", "ShortDot")
$.PlotMultHLine("卡玛利拉枢纽点", parseFloat(s3).toFixed(2), "S3", "green", "ShortDot")
$.PlotMultHLine("卡玛利拉枢纽点", parseFloat(s4).toFixed(2), "S4", "green", "ShortDot")
}
function demapivot(Rdata){
var prerdata = Rdata[Rdata.length - 2];
// 最高价(H)、最低价(L)、收盘价(C)、开盘价(O)
var high = prerdata['High'];
var low = prerdata['Low'];
var close = prerdata['Close'];
var open = prerdata['Open'];
// 计算 "X" 值
var X;
if (close < open) {
X = high + 2 * low + close;
} else if (close > open) {
X = 2 * high + low + close;
} else {
X = high + low + 2 * close;
}
// 计算枢轴点(PP)
var PP = X / 4;
// 计算阻力位(R1)
var R1 = X / 2 - low;
// 计算支撑位(S1)
var S1 = X / 2 - high;
$.PlotMultRecords("德马科麦枢纽点", "KLine", Rdata, {layout: 'single', col: 12, height: '1200px'})
$.PlotMultHLine("德马科枢纽点", parseFloat(PP).toFixed(2), "P", "green", "ShortDot")
$.PlotMultHLine("德马科枢纽点", parseFloat(R1).toFixed(2), "R1", "green", "ShortDot")
$.PlotMultHLine("德马科枢纽点", parseFloat(S1).toFixed(2), "S1", "green", "ShortDot")
}
这段代码提供了四种不同枢轴点的计算公式,并通过$.PlotMultRecords和$.PlotMultHLine函数将枢轴点及其对应的支撑阻力水平绘制到K线图上。不同枢轴点计算方式虽然各不相同,但它们都能提供价格的重要参考点,帮助交易者判断市场走势。
在DATADATA平台,我们同样引入了不同类型枢纽点的参考工具,大家可以输入指定的参数,进行不同类型枢纽点的参考。
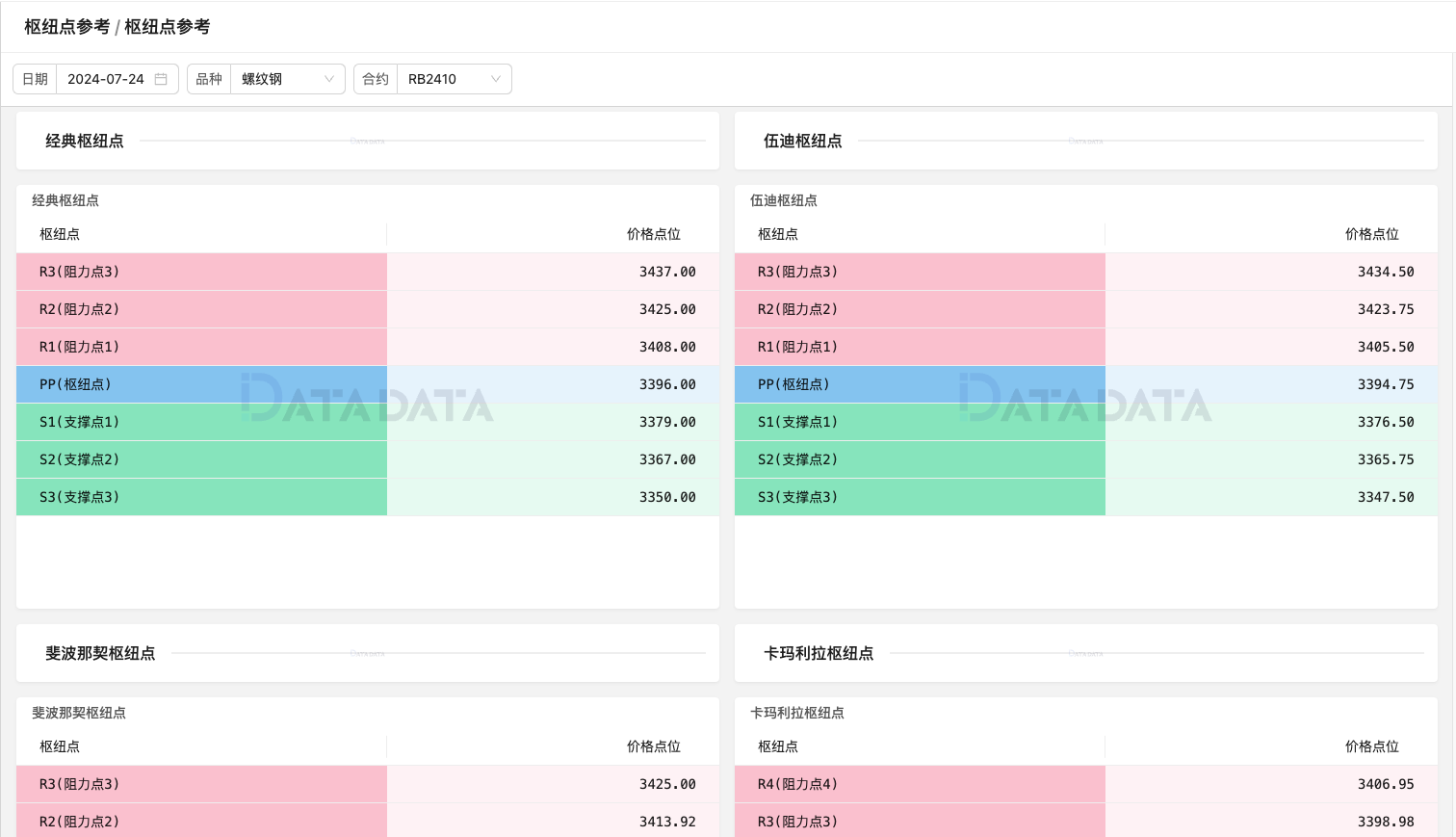
- 国庆礼包:穿越牛熊市!网格交易策略揭秘与收益实战
- 深度解析商品期货中的胜率与盈亏比:交易策略成败的关键
- 商品期货风险控制:一个函数挽救400W的损失
- 优宽量化平台与CTP系统接口的深度融合及应用指南
- 商品期货「订单流」系列文章(四):微单和POC
- 探索优宽量化:状态栏按钮的全新应用(一)
- 商品期货「订单流」系列文章(三):供需失衡和堆积带
- 详解优宽量化交易平台API升级:提升策略设计体验
- 商品期货「订单流」系列文章(二):Delta指标
- 商品期货「订单流」系列文章(一):订单流概念介绍
- 利弗莫尔买入法原理及其在商品期货市场的应用
- 商品期货中‘盈利加仓,亏损减仓’策略示例
- 点石为金:如何让一个指标“化腐朽为神奇”
- 公平价值缺口 (FVG) 检测与过滤:基于 ICT 概念的应用
- 嗤之以鼻 or 逐浪学习:浅谈波浪理论在商品期货市场中的应用
- 策略界面参数与交互控件新增功能详解
- 浅谈期权交易策略在不同市场行情中的应用
- 浅谈商品期权市场中的隐含波动率微笑曲线
- 浅谈商品期权市场平仓操作盈亏估算方法
- ICT交易系统:导入部分