简单的贝叶斯定理理解与商品期货应用实践讨论

简单的贝叶斯定理理解与商品期货应用实践讨论

本篇文章我们一起来讨论一些关于概率的内容。贝叶斯定理可能大家经常关注“概率”、“统计”、甚至“机器学习”方面的内容时会听到，关于这个公式的推导是比较复杂的，所以这里不再赘述。我们来换个角度讲一点简单、容易的理解。

贝叶斯公式

P(A|B) = P(B|A) * P(A) / P(B) 

这个公式看起来很简单，我们通过一个模型来理解。

我们假设在一个平面上有2个面积不同的圆，即圆A，圆B。这两个圆有相交部分。然后这个平面上方开始随机位置掉落小球，一共掉落了N个小球。其中落到圆A中的小球个数为NA个，落入圆B中的小球有NB个，落入圆A、圆B相交部分的小球有NAB个。

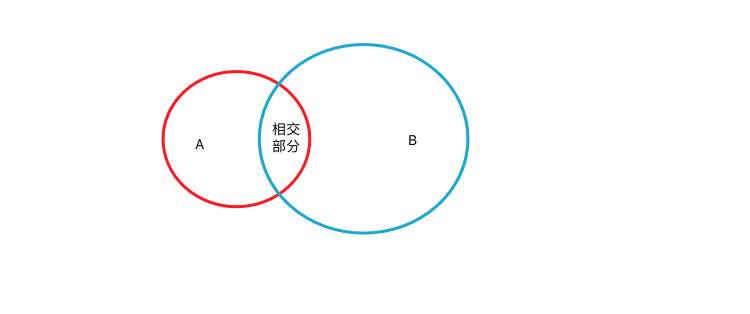
那我们就可知：

• 小球落入圆A并且落入圆A、圆B相交部分的概率为： P(B|A) = NAB / NA
• 小球落入圆B并且落入圆A、圆B相交部分的概率为： P(A|B) = NAB / NB

P(B|A) * NA = NAB = P(A|B) * NB
P(B|A) * NA / N = P(A|B) * NB / N  // 等式两边同时除以N。
P(B|A) * P(A) = P(A|B) * P(B)      // NA / N 就是小球掉落到圆A的概率，NB / N 同理。
P(B|A) * P(A) / P(B) = P(A|B)
P(A|B) = P(B|A) * P(A) / P(B)

发现这个模型等式，最后变形之后就是贝叶斯定理公式。

商品期货市场上的简单应用

那么这个公式有什么用呢？日常的应用场景有垃圾邮件识别，例如：

引用知乎上的回答，假设我们有很多邮件，每封邮件都已经标记好了垃圾邮件标记。我们很容易计算出以下概率：

• P(A)即垃圾邮件的概率，算法：垃圾邮件数量/所有的邮件数量。
• P(B)即邮件中出现词W的概率，算法：出现词W的邮件数量/所有的邮件数量。
• P(B|A) = 垃圾邮件中出现词W概率，算法：垃圾邮件中含有词W的邮件数量/所有的垃圾邮件数量。

可能您会问，P(B|A)不是可以用P(A)和P(B)计算出来么？确实可以，不过此处的P(B|A)并不是由基础的P(A)和P(B)计算得出。而是由样本中大量的数据统计而来的概率。我们由上述的三个概率可以得出，出现词W的邮件是垃圾邮件的概率：

P(A|B) = P(A)*P(B|A)/P(B) = 邮件中出现词W的概率 * 垃圾邮件中出现词W概率 / 是垃圾邮件的概率

这个模型中对垃圾邮件学习的过程就是计算P(A|B)的过程。一封垃圾邮件中会有很多词被包含，所以需要不断地尝试不同词组的组合，直至找到概率大于预期概率的词W或一组词W1，W2等。然后就可以用得到的词计算，判断新的邮件是不是垃圾邮件。

商品期货上我们可以来判断不同品种的行情相关性，例如我们判断如果rb螺纹钢当前BAR是阳线，那么hc热卷当前BAR也是阳线的概率。

下面来动手构建这个程序模型，youquant.com策略源码：

/*backtest
start: 2022-04-01 09:00:00
end: 2022-04-25 15:00:00
period: 1d
basePeriod: 1h
exchanges: [{"eid":"Futures_CTP","currency":"FUTURES"}]
*/

function test(pRa, pRb) {
    if (pRa.length < 100 || pRb.length < 100 || pRa[pRa.length - 1].Time != pRb[pRb.length - 1].Time) {
        return 
    }
    
    // 检查
    var ia = pRa.length - 1
    var ib = pRb.length - 1
    while (1) {
        if (pRa[ia].Time != pRb[ib].Time) {
            Log(ia, ib, _D(pRa[ia].Time), _D(pRb[ib].Time))
            throw "检查不通过"
        }
        if (ia == 0 || ib == 0) {
            break
        }
        ia--
        ib--
    }

    var sumPlusA = 0
    var sumPlusB = 0
    var sumPlusAB = 0
    
    var maxLen = Math.min(pRa.length, pRb.length)
    
    ra = []
    rb = []
    for (var i = pRa.length - maxLen ; i < pRa.length ; i++) {
        ra.push(pRa[i])
    }
    for (var i = pRb.length - maxLen ; i < pRb.length ; i++) {
        rb.push(pRb[i])
    }
    
    for (var i = 0 ; i < ra.length ; i++) {
        if (ra[i].Close > ra[i].Open) {
            sumPlusA++
        }
        if (rb[i].Close > rb[i].Open) {
            sumPlusB++
        }
        if (rb[i].Close > rb[i].Open && ra[i].Close > ra[i].Open) {
            sumPlusAB++
        }
        
        if (ra[i].Time != rb[i].Time) {
            Log(_D(ra[i+1].Time), _D(rb[i+1].Time), i+1)
            Log(ra.length, rb.length, _D(ra[i].Time), _D(rb[i].Time), maxLen, i, pRa.length, pRb.length)
            throw "ra[i].Time != rb[i].Time"
        }
    }


    var p_a = sumPlusA / ra.length
    var p_b = sumPlusB / rb.length
    var p_ba = sumPlusAB / sumPlusA

    var p_ab = p_a * p_ba / p_b
    Log("p_ab:", p_ab, "p_a:", p_a, "p_ba:", p_ba, "p_b:", p_b)
    return p_ab
}


function main() {    
    while (1) {
        if (exchange.IO("status")) {
            exchange.SetContractType("rb2205")
            var ra = exchange.GetRecords()
            exchange.SetContractType("hc2205")
            var rb = exchange.GetRecords()
            var ret = test(ra, rb)
            LogStatus(ret)
        }
        Sleep(500)
    }
}

代码中做了一些K线数据对齐的判断、处理。

main函数里订阅了2个合约的数据：

            exchange.SetContractType("rb2205")
            var ra = exchange.GetRecords()
            exchange.SetContractType("hc2205")
            var rb = exchange.GetRecords()

订阅了螺纹钢2205合约、热卷2205合约。

回测运行：

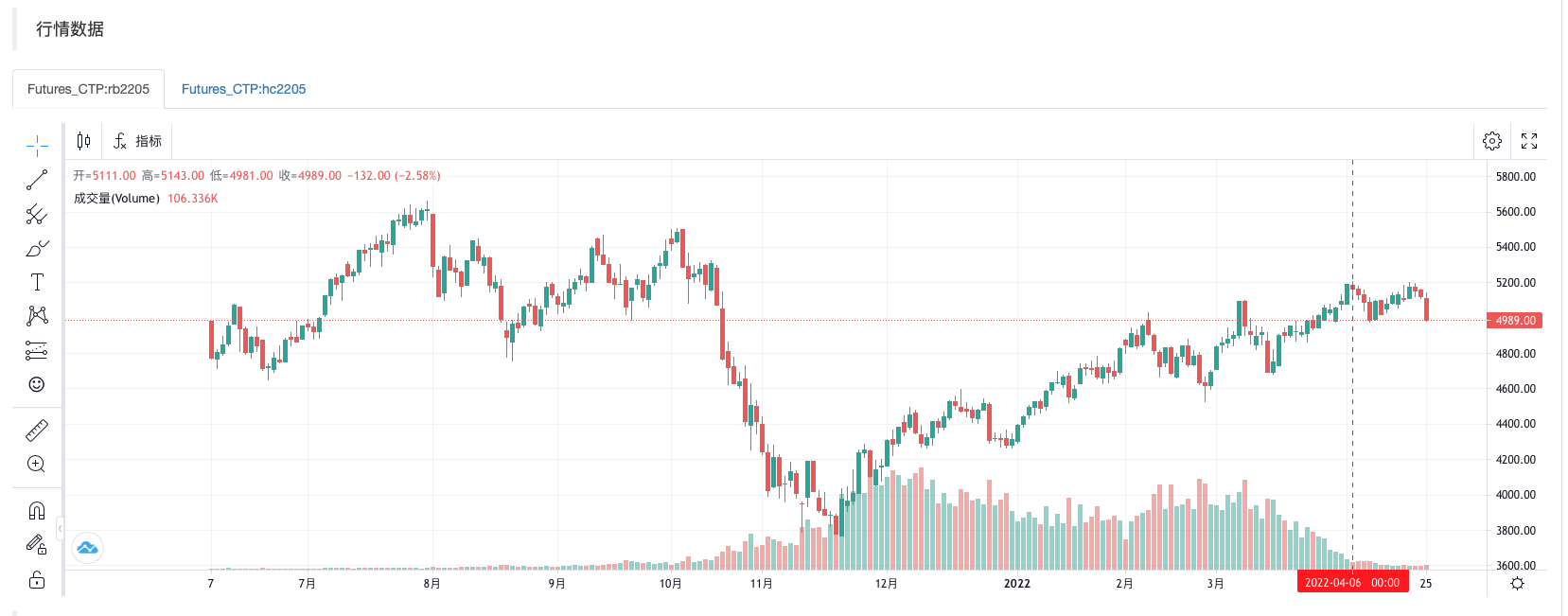
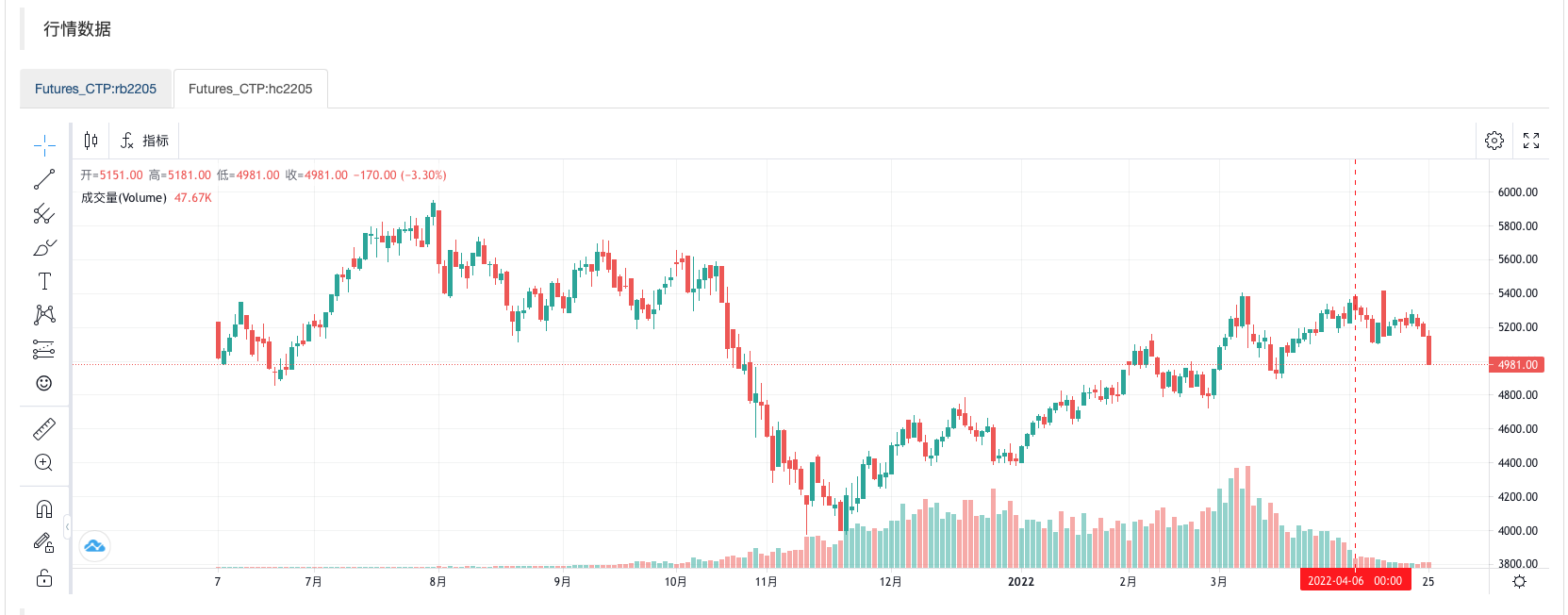
从K线图表上可以看出行情比较类似。

得出的结果，0.9322033898305083 即：热卷当前BAR是阳线，螺纹钢当前BAR也是阳线的概率。说明这两个品种行情相关性很高。

我们可以试下一个和rb螺纹钢不相关的品种，例如鸡蛋，jd2205合约。

结果就说明，这两个合约相关性很差了。

甚至我们还可以试下rb2205和rb2210。

算出P(A|B)为：0.9365079365079366，可见即使是同样的品种的合约，不同交割期的合约行情也存在偏差的可能，跨期套利的机会与风险就在于此。

以上就是小编我在youquant.com上学习量化、程序化时的一些心得记录。如有错误，欢迎各位大神指出，相互学习，一起进步！